地理学的里奇流（Ricci flow）方法——理论、应用与前景

　　地理学的里奇流（Ricci flow）方法——理论、应用与前景

　　李后强（成都市社会科学界联合会主席、四川省社会科学院教授）

　　第宝锋（四川大学-香港理工大学灾后重建与管理学院院长、教授）

　　里奇流（Ricci flow）方法作为一种源自微分几何的强大分析工具，正日益展现出在地理学研究中的巨大潜力。我们系统阐述了里奇流的基本概念、核心方程与主要原理，重点分析了其与地理学的内在关联及应用前景。研究表明，里奇流通过模拟地理系统随时间演化的内在规律，为理解区域发展不平衡、环境演变过程及空间结构优化等地理问题提供了新颖的定量分析框架。我们还探讨了里奇流方法在区域协调发展、地形演化模拟、城市空间结构优化等多个地理学领域的具体应用路径，为地理学研究范式的创新提供了理论支持。

　　1. 引言

　　微分几何学作为研究空间形态与性质的重要数学分支，自17世纪发展以来，为诸多学科提供了丰富的分析工具与理论支撑。里奇流方法作为微分几何中的核心概念之一，由数学家理查德·汉密尔顿于1982年正式提出，并在格里戈里·佩雷尔曼证明庞加莱猜想的过程中发挥了关键作用，引起了全球数学界的广泛关注。近年来，这一方法开始超越纯数学领域，在物理学、工程学以及地理学等学科中展现出强大的应用潜力。

　　地理学作为研究地球表层空间分异规律的科学，始终致力于发展新的理论框架以解释日臻复杂的地理现象。传统地理学理论在宏观和中观尺度上取得了显著成就，但在微观尺度上面临着诸多挑战，尤其是对连续地理现象的刻画和非线性关系的表达。里奇流方法通过描述流形上度量随时间的演化规律，为地理系统研究提供了新的视角。

　　我们探讨里奇流方法在地理学中的应用价值，包括其数学基础、核心原理、与地理学的内在关联以及具体应用领域。这一探索不仅有助于深化对地理系统复杂性的理解，也为地理学研究提供了新的方法论工具，具有重要的理论价值与实践意义。

　　2. 什么是里奇流方法

　　2.1 基本概念

　　里奇流是一种几何演化方程，属于微分几何学中几何分析领域的重要工具。其核心思想是通过描述流形上度量张量随时间的变化，使流形的曲率逐渐均匀化，最终达到规则状态。从直观上看，里奇流可以类比于热传导方程，如同热量从高温区域向低温区域扩散一样，里奇流使流形的高曲率区域向低曲率区域传播曲率，最终实现曲率的均衡分布。

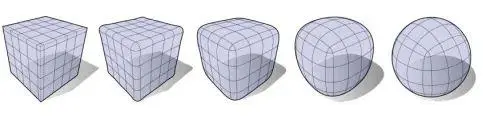
　　流形是里奇流方法的核心概念，指的是一种在局部范围内近似于欧几里得空间的拓扑空间。地球表面就是一个典型的二维流形实例——虽然整体是一个弯曲的曲面，但在局部小范围内可以被视为平面。这一特性使得流形成为描述地理空间的理想数学工具，因为地理空间同样具有局部简单、全局复杂的特征。

　　2.2 核心方程

　　里奇流的基本方程是一个非线性偏微分方程，由汉密尔顿于1982年提出。其最简单形式表示为：

　　∂g_ij/∂t = −2R_ij

　　其中，g_ij是流形的度量张量，表示流形上点之间的距离关系；R_ij是里奇曲率张量，描述流形的弯曲程度；t是描述流形演化的参数，通常被解释为时间。该方程表明，度量张量随时间的变化率与负的里奇曲率张量成正比。这意味着高曲率区域的度量收缩较快，而低曲率区域的度量收缩较慢，从而导致曲率逐渐均匀化。这一过程类似于地理学中的扩散过程，如人口扩散、信息传播等，使里奇流与地理过程之间建立了天然联系。

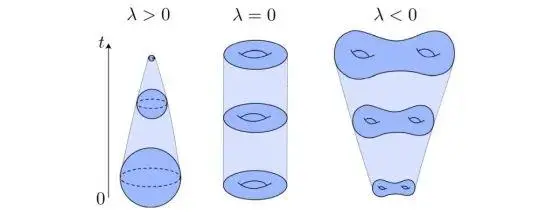
　　2.3 几何原理

　　从几何角度看，里奇流会使流形经历一系列连续的变形过程。正曲率区域在流的作用下会收缩，而负曲率区域则会扩张。这一过程可以通过佩雷尔曼的肥皂泡比喻直观理解：当吹动一个不规则形状的肥皂泡时，表面张力会使肥皂泡逐渐变为完美的球形。类似地，里奇流通过曲率驱动演化，使流形趋向于均匀曲率的状态。

　　值得注意的是，里奇流具有内蕴性，即它仅依赖于流形本身的几何性质，无需外部参照系。这一特性使其特别适合描述地理系统的内在演化规律，因为地理演变同样主要受内部动力驱动。

　　3. 里奇流方法的主要原理

　　里奇流方法建立在几个核心原理之上，这些原理不仅体现了其数学本质，也奠定了其在地理学中应用的基础。

　　3.1 基本特性

　　里奇流具有六个关键特性，使其成为研究流形的强大工具。

　　1.内蕴性。作为黎曼流形上的内蕴几何流，里奇流仅依赖流形本身的几何性质，无需额外坐标系或外部参照。这一特性与地理系统的自组织性高度契合，因为地理演变同样主要由内部因素驱动。

　　2.演化性。随着时间推进，里奇流能消除局部不规则性，同时保持拓扑结构不变。这意味着地理实体在演化过程中可能改变形状和大小，但基本连接关系得以保持。

　　3.直观性。里奇流提供了一种直观的方法来研究流形的几何化、收敛性及分类，使复杂的空间问题可以通过几何直观来理解。

　　4.物质性。里奇流与爱因斯坦引力方程、弦论中的伸缩子场相关，可用于模拟时空演化及物质分布，为物理地理学现象提供解释框架。

　　5.能动性。里奇流可以实施“手术”改变现状，避免演化中出现“奇点”，以保持整体性和连续性。这一特性对于处理地理系统中的突变现象具有重要意义。

　　6.敏感性。里奇流对于初始条件非常敏感，不同初始量可能导致截然不同的结果。这对应了地理系统中的路径依赖现象，即微小初始差异可能导致完全不同的发展轨迹。

　　3.2 熵单调性原理

　　佩雷尔曼在里奇流研究中引入了熵单调性原理，这是他对里奇流理论的重要发展。熵在里奇流中是非减的，随着流的演化，系统的熵值不断增加，标志着系统从有序向无序演化的趋势。然而，在特定条件下（如老窖微生物系统），系统可能出现熵减现象，表示有序性增加。这一原理为理解地理系统的演化方向提供了新视角。例如，区域发展不平衡可以视为一种高熵状态，而通过合理的政策干预（类似里奇流中的“手术”），可以引导系统向低熵的有序状态发展。

　　3.3 奇点分析与手术过程

　　在里奇流演化过程中，可能会出现奇点，即曲率趋于无穷大的点。汉密尔顿和佩雷尔曼发展了奇点分析理论，并引入了“拓扑手术”概念。当流形某部分曲率过大时，可以实施手术，切除奇点区域，并用更规则的几何结构替代，然后继续演化。这一过程与地理系统中的变革性规划有相似之处。例如，当某区域发展出现严重失衡（类似奇点）时，可能需要实施重大干预措施（类似手术），如政策调整、重大项目布局，以重塑区域发展格局。

　　4. 里奇流方法解决的核心问题

　　里奇流方法最初是为了解决数学中的核心问题而发展的，但其解决问题的能力使其在地理学中同样具有广泛应用前景。

　　4.1 庞加莱猜想与几何化问题

　　庞加莱猜想是拓扑学中的百年难题，内容为——每个单连通的、闭合的三维流形都同胚于三维球面。佩雷尔曼通过里奇流方法成功证明了这一猜想，展示了里奇流在处理复杂空间形态方面的强大能力。

　　在地理学中，类似的问题包括——如何判断一个地理区域在连续变形下是否等价于某个标准形状？如何将复杂的地理空间简化为基本几何形态？里奇流方法为处理这类问题提供了数学工具。

　　4.2 曲率均匀化与不规则性消除

　　里奇流核心功能之一是消除不规则性，使流形曲率趋于均匀。这一功能对应地理学中的区域均衡发展问题。例如，四川中东西部构成一个几何流形，各地曲率不同，经济发展水平各异，通过实施“四化同步、城乡融合、五区共兴”等战略，可以促进区域协调发展，把“低洼”（凹陷）变为“高地”（凸出）。

　　4.3 流形分类与结构识别

　　里奇流方法有助于对流形进行系统分类和结构识别。通过研究里奇流的演化路径和最终状态，可以判断流形的本质特征和分类归属。在地理学中，这一能力可用于区域类型划分和空间结构识别。例如，通过分析地形演化过程，可以识别不同地貌类型的本质特征和演化规律。

　　4.4 多尺度分析与尺度推绎

　　里奇流方法天然支持多尺度分析，因为流形在演化过程中会经历不同尺度上的变化。这一特性对于地理学中的尺度推绎问题具有重要意义。通过里奇流方法，可以将微观地理过程与宏观地理格局联系起来，实现跨尺度的地理现象解释。

　　5. 里奇流与地理学的关联

　　里奇流方法与地理学之间存在深刻的内在联系，这种联系为里奇流在地理学中的应用奠定了坚实基础。

　　5.1 共同的研究对象：空间与形态

　　地理学与里奇流方法都关注空间与形态的研究。地理学考察地球表面的空间分异规律，而里奇流研究流形的几何形态演化。这种研究对象的相似性使两者具有天然的亲和性。例如，地球表面本身就是一个二维流形，其形态演化既受地理过程影响，也遵循一定的几何规律。

　　5.2 系统观念的契合

　　里奇流方法体现的系统观念与地理学的整体性思维高度契合。里奇流将流形视为一个整体系统，其各部分的演化相互关联、相互影响。类似地，地理学将区域视为一个复杂系统，系统内各要素通过物质流、能量流和信息流相互连接。我们曾经用里奇流方法思考四川“四化同步、城乡融合、五区共兴”发展战略，体现了系统观念在地理学中的应用。区域协调发展需要遵循“差异协同”原则，抛弃“零和博弈”，建立利益共享机制，这与里奇流追求曲率均衡的理念不谋而合。

　　5.3 动态演化视角

　　里奇流与地理学都强调动态演化视角。地理环境并非静态不变，而是处于持续演化过程中。类似地，里奇流描述了流形随时间的演化规律。这种动态视角使里奇流特别适合描述地理系统的时间变化，如城市扩张、环境变迁、经济发展等过程。

　　5.4 从定性到定量的桥梁

　　传统地理学研究较多依赖定性描述，而里奇流方法为地理学提供了严格的定量工具。通过里奇流方程，可以将地理演化过程转化为数学表达，从而实现精确的模拟和预测。这一转变有助于提升地理学的科学性和预测能力，使地理学从描述性科学向精确科学迈进。

　　表：里奇流概念与地理学概念的对应关系

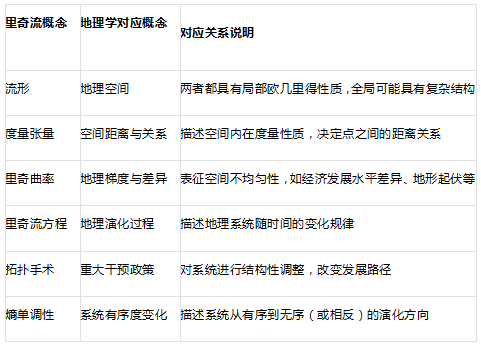
　　6. 里奇流方法在地理学中的应用领域

　　里奇流方法在地理学中具有广泛的应用潜力，以下将探讨几个主要的应用领域。

　　6.1 区域发展与空间规划

　　里奇流方法为区域发展不平衡问题提供了新的分析框架。以四川省为例，其内部各区域经济发展水平差异较大，可以视为一个曲率不均的流形。通过应用里奇流方法，可以模拟区域协调发展路径，识别关键障碍点，并设计有效的干预策略。

　　在“五区共兴”战略中，针对成都平原、川南、川东北、攀西、川西北五大经济区的禀赋差异，可以运用里奇流原理，制定差异化政策，推动全域共兴。例如，对成都平原经济区采取“研发在成都、转化在周边”模式，推动产业链跨区域布局；对攀西经济区依托安宁河流域高质量发展，打造国家战略资源创新开发试验区。

　　6.2 地形演化与环境变迁

　　里奇流方法可以用于模拟地形演化过程。地形变化是一个缓慢而复杂的过程，受内外营力共同作用。通过将地表形态视为二维流形，应用里奇流方程，可以模拟地表侵蚀、沉积和构造运动等地形演化过程。

　　例如，对海螺沟冰川区的地形变化进行研究，可以结合同位素水文分割方法，利用里奇流模拟冰川退缩对地形的影响，预测未来变化趋势。这类研究对理解全球变化下的地理响应具有重要意义。

　　6.3 城市空间结构与网络优化

　　城市系统可以视为复杂的空间网络，其演化规律可以用里奇流方法进行分析和优化。城市空间结构的形成是一个自组织过程，通过里奇流可以模拟城市扩张、功能区演变以及交通网络优化等过程。

　　在“城乡融合”研究中，可以将城市和乡村视为一个整体流形，通过里奇流分析城乡要素流动路径，优化基础设施布局，促进城乡融合发展。例如，通过“县城精修细补十项民生工程”，提升县域教育、医疗等公共服务能力，实现城乡基础设施“无缝对接”。

　　6.4 生态环境与资源管理

　　里奇流方法在生态环境研究中也具有应用价值。生态系统可以视为一个复杂的功能流形，其内部各要素之间存在密切的相互作用。通过里奇流方法，可以模拟生态系统的演化过程，预测生态响应，指导生态修复。

　　例如，在老窖微生物系统研究中，里奇流概念被用于解释微生物群落的协同进化过程。窖泥中的微生物系统存在耗散结构和协同效应，随着时间推移，系统熵减，有序性增强，规则性提高。类似原理可以应用于更广泛的生态系统研究，如生物多样性保护、生态网络构建等。

　　6.5 地理系统模拟与预测

　　里奇流方法为地理系统模拟提供了数学基础。通过建立地理系统的里奇流模型，可以实现对地理过程的定量模拟和预测。这类模型可以考虑地理系统的多重反馈和非线性特征，比传统模型更能反映真实地理过程的复杂性。

　　例如，在气候变化研究中，可以将气候系统视为一个高维流形，通过里奇流模拟不同排放情景下的气候响应，为适应和减缓气候变化提供科学依据。

　　表：里奇流方法在地理学中的应用案例与实现路径

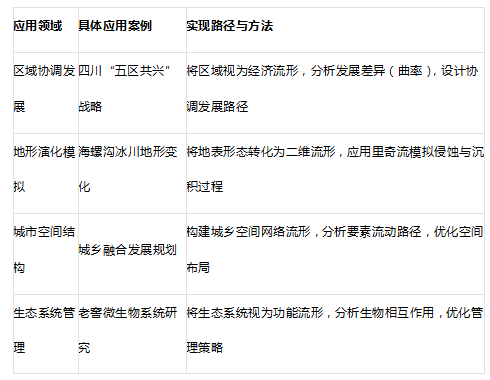
　　7. 结论与展望

　　里奇流方法作为微分几何学中的强大工具，在地理学研究中展现出巨大的应用潜力。本文系统阐述了里奇流的基本概念、核心原理及其与地理学的内在关联，并探讨了其在地理学多个领域的具体应用路径。研究表明，里奇流方法为地理学研究提供了新的视角和工具，有助于提升地理学的精确性和预测能力。

　　里奇流方法的核心优势在于其系统性和动态性，能够将地理系统视为一个整体，分析其内在演化规律。这一特点使里奇流方法特别适合处理地理学中的复杂系统问题，如区域协调发展、环境变迁、城市演化等。同时，里奇流提供的定量工具有助于推动地理学从定性描述向定量分析转变，增强地理学的科学性和应用价值。

　　未来里奇流方法在地理学中的应用可以在以下几个方向继续深入。一是发展更完善的地理流形重构和参数化方法，提高模型的准确性；二是建立流形几何参数与地理过程参数之间的定量关系，增强模型的解释力；三是拓展里奇流方法在应用地理学领域的应用，解决实际地理问题；四是探索里奇流理论与大数据、人工智能等新技术的融合创新，发展智能地理分析工具。

　　随着理论的不断完善和应用技术的持续创新，里奇流方法有望成为地理学研究的重要范式之一，为理解和解决复杂地理问题提供越来越重要的支持。同时，这一跨学科探索也将丰富数学本身的发展，体现基础科学与应用科学相互促进的良性循环。（2025年12月20日）